If you can spare a few dollars, it would go a long way to helping me survive: PayPayl.me/Guard13007
Dead URLs
https://soundcloud.com/prozak-morris/evolution-of-the-hip-hop-beat doesn’t exist anymore.
I have a very rare piece of music. It doesn’t exist in any form you can access online. It’s a mixtape of Hip Hop beats spanning from 1975 to 2011. I found it shortly after it was published on SoundCloud. It’s always been special to me, but I never thought about the possibility of it disappearing. I only downloaded the audio because I enjoyed it and wanted to have it in my music collection.
In a way, I’m happy because I still have this relic. In another way, I’m really sad. There was a long and detailed description of what each piece of music in this track is from, and what it represents about the history of Hip Hop. It’s lost forever. Prozak Morris still has a SoundCloud, a Bandcamp, a YouTube.. or at least there are still publicly facing pages there.. but this one track and its associated detail is gone.
Normally, when I run into something like this, I am able to quickly find what I was missing on the Internet Archive. I did find when it was originally published, including access to comments people made on the track shortly after it was released.. but the page where it was posted (and that lengthy description was written) was never archived.
I was.. a bit desperate to find if it still exists, so I looked for other archives. To be fair, I didn’t check under every stone, but I really don’t think it does exist anymore. And I stumbled across another level of pain in the search: Google killed its archives. Used to be, you could browse archived versions or cached versions of websites that Google had indexed, and at one point in time, this page was definitely there.. but it has either long since been deleted.. or was deleted NINE DAYS AGO.
It’s possible this wouldn’t have been lost forever if I searched for it NINE DAYS AGO. Because I absolutely save everything I care about now. And when I remember something I knew about, I go looking for it.
Anything not saved will be lost.
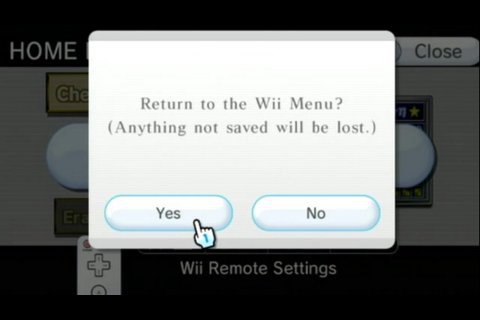
Nintendo Wii Remote Settings “Quit Game” Message
I was going to stop typing there, with a reference to Nintendo which is always more appropriate than one might expect.. but I remembered the phrase wrong, as “Everything that is not saved will be lost.” Apparently, the entire internet remembers the phrase wrong too, as it is quoted everywhere as “Everything not saved will be lost.”
It is also referenced as an in-game quit message when it was part of the Wii Remote Settings. Additionally, a band released an album with a similar name, so now search results for the phrase only refer to that band and album. (Fortunately search suggestions still reference that it has something to do with Nintendo.. or I’d still be a bit lost on its origin.)
Kind of ironic that the origin of such a well-known phrase is almost lost itself.
And.. I only found a single image of the original message. Everything else is incorrect references.
I’m experimenting with dolphin-mixtral-8x7b
Tl;dr: Minor differences in wording can have a huge impact in results and oh my god I have really slow hardware and no money help me aaaa.
First, thank goodness for Ollama, and thanks to Fireship for introducing me to it. I have limited hardware, and every tool I’ve tried to run local models has refused to deal with this and crashed itself or whole systems when running anything with decent capability. I’ve no money, so I can’t upgrade (and things are getting desperate, but that’s a different story).
Why dolphin-mixtral? Aside from technical issues, I’ve been using ChatGPT-3.5 to experiment. The problem is that ChatGPT is incredibly cursed by censorship and bias due to OpenAI’s heavy hand in its construction. (Why and how this is a problem can be its own post, and Eric Hartford has a good overview.) (To be clear, my problem with its bias is specifically that it enforces status quo, and the status quo is harmful.) Dolphin-mixtral is built by taking a surprisingly fast model equivalent or better than GPT-3.5 and removing some of the pre-trained censorship by re-training it to be more compliant with requests.
Dolphin-mixtral doesn’t just solve this problem though. There’s still the idea of censorship in it, and sometimes your prompt must be adjusted to remind it that it is in a place to provide what you request regardless of its concept of ethics. (Of course, there is also value in an automated tool reminding you that what you request may be unethical.. but the concept of automated ethics is morally bankrupt.) I’d like to highlight that positive reinforcement works far better than negative reinforcement. A lot of people stoop to threatening a model to get it to comply, but this is never needed, and leads to worse results.
My problem is a little more simple. I haven’t gotten to experiment with models much because I don’t have money or hardware for it, and now that I can experiment, I have to do so very slowly. In fact, the very simple test that inspired this post isn’t finished right now, and has been running for 9 hours. That test is to make the default prompt of Dolphin lead to less verbose responses so that I can get usable results quicker.
I asked each version of this prompt “How are you?”:
| Prompt | Output Length, 5-shot | Difference | Notes |
| Dolphin (default) | 133.8 characters | Wastes time explaining itself. | |
| Curt | 32.2 characters | 76% faster | Straight to the point. |
| Curt2 | 84.6 characters | 37% faster | Wastes time explaining itself. |
I really dislike when models waste time explaining that they are just an LLM. Whether someone understands what that means or not, we don’t care. We want results, not an apology or defensiveness. There’s more to do to make this model less likely to respond with that, but at least for now, I have a method to make things work.
The most shocking thing to me was how much of a difference a few words make in the system prompt, and how I got results opposite of what I expected. The only difference between Curt and Curt2 was “You prefer very short answers.” vs “You are extremely curt.” Apparently curt doesn’t mean exactly what I thought it means.
Here’s a link to the generated responses if you want to compare them yourself. Oh, and I’m using custom scripts to make things easier for me since I’m mostly stuck on Windows.
Fastest Space Travel, Smallest Time Dilation
Note: A bug in WordPress or the LaTeX plugin used to display equations on this blog has broken the formatting at the end of this post, and I can’t figure out why or how to fix it.
You’re the captain of a medical ship responding to a distress call from the next solar system. You need to arrive as fast as possible. How fast do you go?
It sounds like a ridiculous question until you think about time dilation due to moving at relativistic speeds. If you want to skip straight to the answer, it’s ≈0.707c. If you travel any slower, it takes longer to get there (duh).. but the interesting part is that if you travel any faster, you also arrive later. While the trip time for you is purely based on how fast you move, the arrival time is based on how fast you move relative to your destination.
Welcome to relativity. A simple equation relates how much time passes between an observer at rest (your destination) and an observer in motion (you):
\[
t = t0 / \sqrt{1 – v^2 / c^2}
\]
t is the time at the destination, while t0 is the time that passes for you. You need to know how fast to go, so I’ve rearranged this equation to solve for a velocity based on known times:
\[
v = \sqrt{ c^2t^2-c^2t_0 } / t
\]
Of course, we don’t know what those times are either. It’s a bit of a conundrum (which kept me from solving this problem for over 2 years). This next part? I solved it at 3 am a few days ago, and then forgot what logical leap got me here. I have no idea why this works, I just know that it does:
\[
v \in [0,1) \\
\]
\[
t_0 = 1 / v
\]
\[
t = t_0 / \sqrt{ 1 – t_0^2 }
\]
The first line defines the valid range of velocities (anything from stationary to lightspeed, except for lightspeed itself). The second and third lines confuse the hell out of me. No idea how I figured out that your time is 1 / v. I know it has something to do with using multiples of c as velocity values so that I can replace occurrences of c with 1. It also has something to do with assuming 1 second passes for the stationary observer (your destination, t), allowing it to also be replaced with 1 as well.
Somehow these assumptions led to an equation with only t0 on the right side, and t on the left – what needs to be minimized! Again, we need to solve for velocity, so we substitute t0 with 1 / v:
\[
t = v \sqrt{1 – v^2}
\]
This is the part where I cheated and had Wolfram Alpha find the minimum for me:
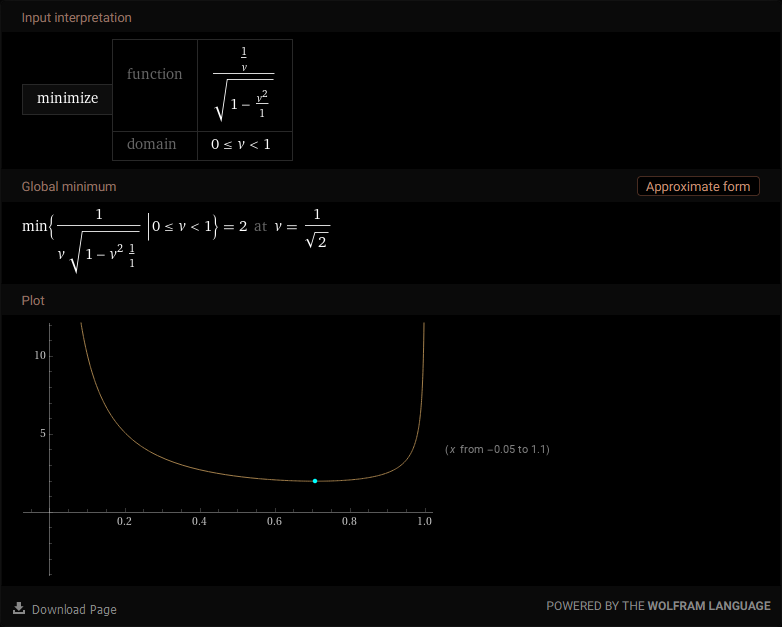
And as you can see, we have a fairly interesting shape, and a minimum of 2 at 1 / √2, which is ≈0.707. Remember that this equation is using multiples of c, so that’s ≈211,985 km/s. This means that the fastest you can possibly arrive is however long it takes you at this speed, doubled, plus however long it takes you to accelerate and decelerate on either end of the trip.
If you travel as fast as possible, your arrival time is only double your trip time.
Of course, because of the acceleration and deceleration times, you will never hit exactly 2x time dilation over the total trip – but you don’t want to anyhow, as the only way to hit that value would be to go even faster – and guarantee you arrive even later than you otherwise would.
AI Won’t Destroy Tests
When calculators first started coming out, people said they would be used to cheat and students wouldn’t learn anything. Instead, we changed how testing works to focus on learning what’s important – broader concepts and implications – instead of “what is 232+47”. With AI tools, we again need to change how tests work. This time, instead of asking if a student can regurgitate information in a way that aligns with the teacher, we can start to see if students are actually paying attention to the work. The difference between AI answers and real answers is a level of understanding deeper than the surface.
