Tag: maths

Posted on

Fastest Space Travel, Smallest Time Dilation

You’re the captain of a medical ship responding to a distress call from the next solar system. You need to arrive as fast as possible. How fast do you go?

It sounds like a ridiculous question until you think about time dilation due to moving at relativistic speeds. If you want to skip straight to the answer, it’s ≈0.707c. If you travel any slower, it takes longer to get there (duh).. but the interesting part is that if you travel any faster, you also arrive later. While the trip time for you is purely based on how fast you move, the arrival time is based on how fast you move relative to your destination.

Welcome to relativity. A simple equation relates how much time passes between an observer at rest (your destination) and an observer in motion (you):

    \[t = t0 / \sqrt{1 - v^2 / c^2}\]

t is the time at the destination, while t0 is the time that passes for you. You need to know how fast to go, so I’ve rearranged this equation to solve for a velocity based on known times:

    \[v = \sqrt{ c^2t^2-c^2t_0 } / t\]

Of course, we don’t know what those times are either. It’s a bit of a conundrum (which kept me from solving this problem for over 2 years). This next part? I solved it at 3 am a few days ago, and then forgot what logical leap got me here. I have no idea why this works, I just know that it does:

    \[v \in [0,1) \\\]


    \[t_0 = 1 / v\]


    \[t = t_0 / \sqrt{ 1 - t_0^2 }\]

The first line defines the valid range of velocities (anything from stationary to lightspeed, except for lightspeed itself). The second and third lines confuse the hell out of me. No idea how I figured out that your time is 1 / v. I know it has something to do with using multiples of c as velocity values so that I can replace occurrences of c with 1. It also has something to do with assuming 1 second passes for the stationary observer (your destination, t), allowing it to also be replaced with 1 as well.

Somehow these assumptions led to an equation with only t0 on the right side, and t on the left – what needs to be minimized! Again, we need to solve for velocity, so we substitute t0 with 1 / v:

    \[t = v \sqrt{1 - v^2}\]

This is the part where I cheated and had Wolfram Alpha find the minimum for me:

Source

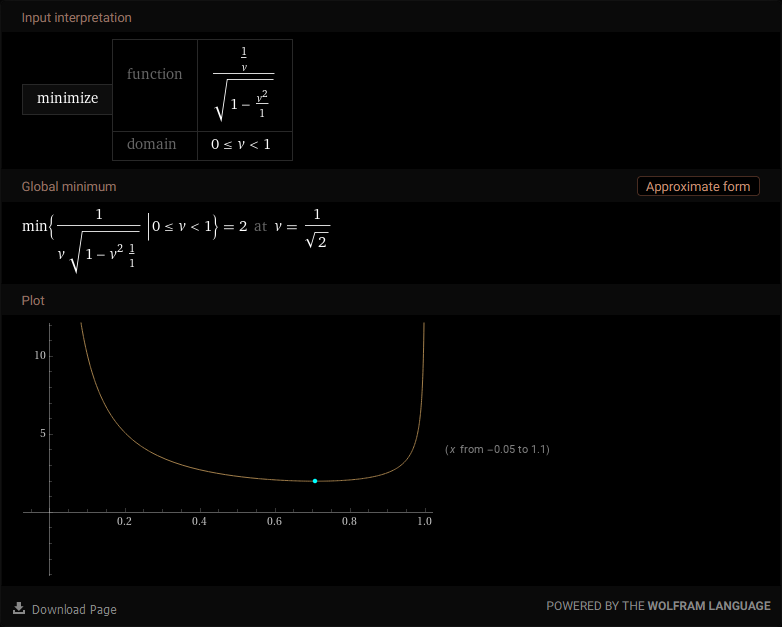
And as you can see, we have a fairly interesting shape, and a minimum of 2 at 1 / √2, which is ≈0.707. Remember that this equation is using multiples of c, so that’s ≈211,985 km/s. This means that the fastest you can possibly arrive is however long it takes you at this speed, doubled, plus however long it takes you to accelerate and decelerate on either end of the trip.

If you travel as fast as possible, your arrival time is only double your trip time.

Of course, because of the acceleration and deceleration times, you will never hit exactly 2x time dilation over the total trip – but you don’t want to anyhow, as the only way to hit that value would be to go even faster – and guarantee you arrive even later than you otherwise would.

Posted on

Semi-Empirical Stellar Equations

I’ve spent a lot of time trying to answer certain questions in astronomy, where I just want a rough approximation for the purpose of a simulation, and don’t need an exact answer. These are some of the equations I’ve come up with.

Yerkes Classes’ T/Mv Relations

These equations are shown as functions where x is temperature in Kelvin, and f(x) is absolute magnitude (visual). Most are valid from 2400 K to a little bit past 30000 K, the exceptions are noted. For the hypergiants and white dwarfs, the range is within an elliptical region, of which these functions define the major axis; for all others, they are a trend line along a Yerkes classification.

  • Hypergiants (0):
    f(x) = -8.9
  • Supergiants (Ia):
    f(x) = -0.00135x3 + 0.0233x2 + 0.0187x – 7.349
  • Supergiants (Ib):
    f(x) = 0.00329x3 – 0.0962x2 + 0.829x – 7.209
  • Bright Giants (II):
    f(x) = 0.00557x3 – 0.166x2 + 1.505x – 6.816
  • Giants (III):
    f(x) = 0.0135x3 – 0.373x2 + 3.019x – 7.233
  • Subgiants (IV):
    f(x) = -0.151x2 + 2.216x – 5.128 (4450-100000 K only)
  • Dwarfs (V):
    f(x) = 0.00193x5 – 0.0615x4 + 0.742x3 – 4.257x2 + 12.439x – 12.996 (note: this one is the least accurate)
  • Subdwarfs (VI):
    f(x) = 0.131x3 – 3.275x2 + 27.576x – 71.7 (3050-6000 K only)
  • White Dwarfs (VII):
    f(x) = 0.489x + 10.01 (4450-30000 K only)

Simple Conversions

  • Absolute Magnitude (visual) → Luminosity (solar luminosities):
    Lsun = 100 * exp(-0.944 * Mv)
    Accurate between 0-10 Mv. Probably continues accuracy relatively well.
  • Main Sequence Luminosity / Mass Relation:
    Lstar / Lsun = (Mstar / Msun)3.5
    Lstar = ( 3.68 * ln(Mstar) – 0.244 )e
    (The second equation applies to all stars.)
  • Mass / Lifetime Relation:
    Tyears = ( 23.4 – 2.68 * ln(Mstar) )e
    (This applies to all stars.)

Spectral filters are used to help classify stars. Ultraviolet, Blue, Visual, Red, and Infrared. Objects are listed in different indexes:

  • U–V for the hottest objects (stellar remnants, galaxies)
  • B–V (the majority of stars)
  • R–I for the coolest (LTY “stars” and below)

Equations I no longer recommend

Provided for completeness, in case they are found to be useful.

  • Temperature (K) → Absolute Magnitude (visual):
    Mv = 35.463 * exp(-0.000353 * T)
    Roughly accurate between 2000-50000 Kelvin. Probably doesn’t continue accuracy at hotter temperatures. Previously this was at the top of this post, now I am not sure why (perhaps the simplicity). The Yerkes’ classifications are a better system.
  • B-V index (x) → Temperature (K):
    T = -772.2x3 + 3152x2 – 6893x + 9500
    Sorta accurate between 0-2. (This equation I am least comfortable with, and don’t plan to use.)
Posted on

I don’t understand lambda calculus

Update, 2024-10-11: Man, this is a garbage post. I was trying to get my thoughts out, but I have next to no clue what I was doing and don’t really understand it. You want to learn about Lambda Calculus? Go anywhere else. Sorry. >.<

I’m playing around in Minetest, and I have an idea. In order to execute this idea, I’m going to need a simple programming language. Asking Google… implementing a simple programming language…

7 lines of code, 3 minutes: Implement a programming language from scratch
Sounds good! Ridiculously simple, fast, and gives us a fully usable language. (I would’ve understood brainfuck better..) Let’s see what this language looks like:

(λ v . e)   anonymous function with argument v and returning e
(f v)       call function f with argument v
(λ a . a)   example: identity function (returns its argument)

And the scary one:
(((λ f . (λ x . (f x))) (λ a . a)) (λ b . b))

Seems okay until I get to understanding that last example. If you’re curious about the steps I went through before I finally figured it out, here are my notes. I’m gonna skip to the good part:

(((λ f . (λ x . (f x))) (λ a . a)) (λ b . b))
two identity functions, let's name them I, & remove excess parenthesis
(λ f . (λ x . (f x))) I I
the syntax is still confusing me, let's make an "F" function
F(x) -> return (λ x . (f x))
F I I                          equivalent to ((F I) I)
substituting the function (identity) into our definition gives us
(λ x . (I x))                  which..is actually the same as the identity function
I(I)                           ..it all comes to returning the identity function

λ x . x

Now, at this point I’ve learned a few small tricks for my understanding, as well as how lambda calculus works in general.

Reduction

Solving a lambda calculus program is made of three (or 2.5) steps called reductions:

  • η-conversion (eta): Replace equivalent functions with simpler forms (λ x . f x) -> f
  • β-reduction (beta): Substitution (λ a . a) x -> x (essentially, THIS is solving it)
  • α-conversion (alpha): Rename conflicting names (λ a . a b) (λ a . a) -> (λ a . a b) (λ c . c)

References

This is where my journey ends for now. I started studying lambda calculus because of a desire to implement a simple programming language, but this will likely not satisfy my needs..at least not in this form. (Note: All resources are archived using the services linked to on Archives & Sources.)

Posted on

My Obsession

(This post has been imported from an old blog of mine.)

For years I’ve been thinking about a rocket construction and flight game. Think 2D Kerbal Space Program, but with part design as well as craft design, and some SciFi aspects to it.

picture of a notebook showing my obsession with spacecraft
Just started on the project again and ran into a problem with the physics library I’m using (box2d), so for kicks I decided to calculate how many shapes I might need to try to make a planetoid have a variable surface instead of being circular.

Basically, a grandiose expansion of the concepts of KSP while simultaneously stepping backwards by making it 2-dimensional instead of within a 3D universe. I am a bit more realistic with my expectations than I previously was, so I know I’m not going to achieve it for a very long time, if ever, but it still is fun to think about or poke around with code or draw out some ideas from time to time.